
À propos de la modélisation des transitoires des sources ponctuelles pour le détecteur LW~ISOCAM
Introduction
La majorite des détecteurs en astronomie Infrarouges embarques sur les satellites (IRAS, ISO, SIRTF, ASTRO-F/AKARI) et fonctionnant entre 5 et 200 microns de longueur d'onde sont affectés par de forts effets de remanence (aussi appelés transitoires ou effets de mémoire (transients, latents or memory effect)).
En 1998, nous avons montré que les transitoires affectants la camera ISOCAM semblaient pouvoir être décrits par un modèle analytique issu de la physique. Peu après, il est devenu evident que ce modèle ne marchait bien que lorsque l'éclairement de la camera est spatialement quasi-uniforme. Il fallait donc chercher un modèle pour decrire les transitoires lorsque le gradient d'éclairement entre pixels voisins est fort, le cas limite étant l'éclairement par une source ponctuelle.
Nous présentons ici les premiers resultats obtenus avec le nouveau modèle de Fouks. Ce modèle a été finalise durant le sejour de 3 mois de B. Fouks sur poste rouge du CNRS à l'IAS.
| Notes de Fouks | Articles (en anglais) | Le modèle et son domaine de validité | Termes correctifs |
| PSFs | Ajustements | Figures | Carte des paramètres du détecteur |
| Travaux à faire | Conclusion |
Notes de Fouks
Les modèles 3D complet et 2D symétrique sont décrits dans les documents ci-dessous. Ce sont des fichiers au format propriétaire MS-Word98. Ils ont été compressés par GZIP.
| Doc 1 : Théorie 1 | Doc 2 : Théorie 2 | Doc 3 : Séminaire A | Doc 4 : Séminaire B |
|---|---|---|---|
| ps2theor.doc.gz (Taille : 204 ko) |
ps5theor.doc.gz (Taille : 99 ko) |
sem-tr1.doc.gz (Taille : 22 ko) |
sem-tr2.doc.gz (Taille : 58 ko) |
Articles (en anglais)
Les trois articles suivant montrent l'évolution de ces travaux sur les 3 dernières années (1999-2001). Ils présentent quelques figures interessantes de transitoires. Le plus récent décrit aussi la methode de correction mise en place. Pour le modèle direct, voir ci-dessus les notes de Fouks. PS: ces articles sont aussi mentionnes sur la page articles ISO.
The three following papers report progress on this problem. The last one contains extensive description of the correction method. For the direct model, please refer to Fouks' notes
| Article 1 SPIE 2000 (Obsolete) | Article 2 Legacy Conference, 2001 (Obsolete, nice figures) | Article 3 Siguenza Conference, 2002 (Etat Actuel / Up to data) |
|---|---|---|
| final_SPIE2.ps.gz (Taille : 117 ko) |
LegConf1.ps.gz (Taille : 114 ko) |
Siguenza2.ps.gz (Taille : 211 ko) |
| final_SPIE.pdf (Taille : 359 ko) |
LegConf1.pdf (Taille : 346 ko) |
Siguenza2.pdf (Taille : 333 ko) |
Le modèle et son domaine de validité
Grâce aux informations précises finalement fournies par le LETI pour la topologie du détecteur ISOCAM, après deux précédents modèles basés sur des informations pas assez precises, B. Fouks a pu développer un modèle de transitoires lorsque l'éclairement spacial de la matrice LW ISOCAM n'est pas uniforme.
À cause des contraintes en temps (développement de la théorie, du code, et des temps de calcul) et de sa volonté d'obtenir une première estimation confirmant ou non son approche (vu les problèmes précédents clairement dus à une mauvaise description/ connaissance du détecteur (sens effectif de polarisation, geométrie des contacts et de la grille réfléchissante, dopage du bulk et des contacts, qualité réelle des contacts, ...)), le domaine de validité du modèle implémenté à partir de sa théorie a été volontairement reduit :
- le cas general 3D est reduit en cas 2D à symétrie circulaire pour le profil des sources;
- le modèle marchera d'autant mieux que le profil de la source sera étroit par rapport à la largeur du pixel.
Cependant, il n'est pas nécessaire que le détecteur soit être stabilisé avant "l'arrivée" de la source.
Néanmoins, les equations 3D développees initialement permettent de traiter des profiles d'éclairement quelconques, ainsi qu'une sequence quelconque d'éclairement. [C'etait un gros travail de simplifier analytiquement de 3D en 2D pour simplifier l'ecriture du code et reduire le temps de calcul, c'est un travail assez important (mais pas enorme) d'ecrire le code 3D à partir des equations 3D inititales.]
Mes excuses (AC), partie inachevée
Dans le détecteur LW ISOCAM, il n'y a pas de separation physique entre pixels. Les pixels sont definis par les contacts implantes par procede de micro-electronique sur les 2 faces du détecteur (un plan continu d'un cote, 32x32 contacts de l'autre, sans parler des vrais-faux pixels de garde, sur les bords) et la polarisation électrique donnant le champ électrique dans le bulk.
Lorsqu'une charge est cree par un photon incident dans le bulk du détecteur, un courant est genere en sortie du pixel correspondant. Mais cette charge est vue aussi par les pixels voisins, et même lointains. Sous éclairement uniforme, ceci n'est pas genant, car ces effets sont moyennes. C'est ce que prend explicitement en compte le modèle 1D de Fouks (Vinokurov & Fouks 1991), abusivement appele modèle de Fouks et Schubert.
Par contre, ceci n'est plus vrai lorsqu'il y a un gradient d'illumination entre pixels voisins. Il est facile de voir cet effet, grâce au jitter du satellite. Le satellite ISO est affecté par un très faible jitter (faible depointage autour de la direction de pointage de reference). Lorsqu'on pointe vers une source ponctuelle, les transitoires des pixels non centraux de la source sont très bruites, sans commune mesure avec le bruit sous éclairement uniforme. Ce bruit est la consequence de l'absence de moyenne sur les courants sous fort gradient. Mais on retrouve ce qui confirme que ce bruit est bien correlé entre les pixels de la source.
Enfin, à l'extrême, lorsque la largeur de la source est petite par rapport à la largeur du pixel, l'effet de moyenne à l'intérieur du pixel redevient , le niveau de bruit et l'overshoot du pixel le plus brillant devrait être beaucoup plus faible que pour un profil de largeur intermediaire.
En résumé, les possibilités et les limites du modèle reduit à 2D sont les suivantes :
- le profil de la source doit être à symétrie circulaire, néanmoins ce profil peut être de forme et de largeur quelconques;
- la position du maximum de ce profil est libre sur la matrice, les pixels eux-mêmes étant sur-echantillonne dans le noyau (kernel) du modèle;
- il est possible de travailler sans être stabilisé avant le changement de profil d'illumination
Termes correctifs
D'après ses hypotheses et limitations, le modèle développé doit decrire d'autant mieux les transitoires que la largeur de la source est étroite par rapport à la taille du pixel.
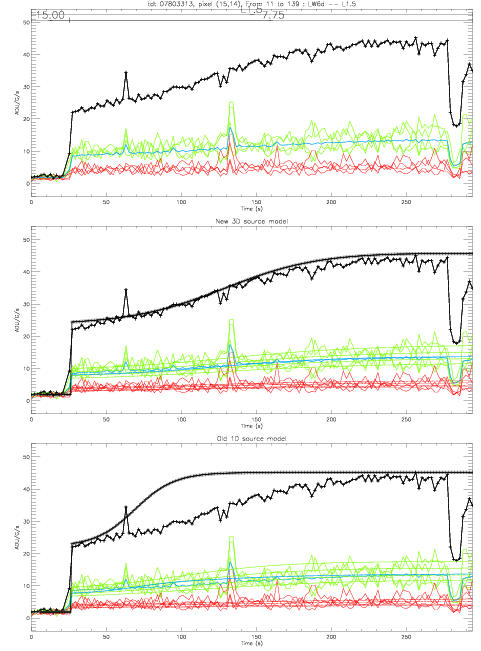
Pour les observations avec les lentilles 12' et 6', tous les filtres donnent des PSF (point spread function) de FWHM (Full Width Half Maximum) inferieures à la largeur du pas du pixel (100 microns) (cf la note technique de K. Okumura sur les PSF). On expere donc un excellent accord données/modèle, pixel par pixel (cf Fig. 3 et Fig. 4).
Pour la lentille 3', il faudra regarder l'accord entre les données et le modèle pour les filtres donnant les plus larges PSF (filtres LW 3, 9, 10).
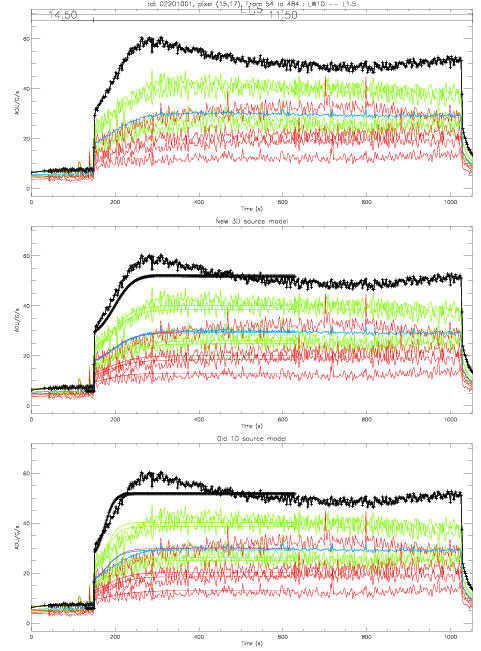
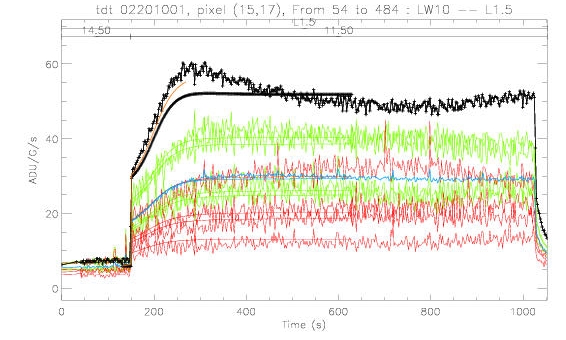
Tres clairement, pour la lentille 1.5' et les filtre donnant les PSFs les plus larges (LW 3, 9, 10), l'accord entre le modèle et les données est mauvais pour le pixel le plus fort. Ceci est illustre sur les figures 1 et 2.
Fouks a développé une correction analytique de premier ordre pour la phase montante du transitoire. Cette correction s'applique pour le pixel le plus fort, avant que le transitoire n'atteigne son premier maximum (cf Fig. 6).
Fouks pense avoir besoin de plusieures semaines pour développer le modèle analytique complet d'ordre 1 de description des transitoires pour les PSFs les plus larges. Il faut noter qu'on perdrait immediatement les simplifications 3D --> 2D dans un tel modèle, car il faudrait tenir compte explicitement de la position de la source d'éclairement dans le pixel.
En conclusion :
- Il est attendu que, plus les PSF sont larges, plus grand est l'écart entre le modèle et les données. Cet effet est clairement observé sur le jeu limite de données étudiées.
- Fouks a développé une première correction analytique simple de cet écart pour le transitoire montant du pixel le plus fort (cf Fig. 6). Cette correction va dans très clairement dans le bon sens pour les données étudiées Il reste un certain travail pour verifier la validité de cet terme de premier ordre sur de nombreuses sources;
- Pensant comprendre l'origine physique des écarts observés, Fouks pense pouvoir développer un modèle complet, il y a néanmoins deux serieux problèmes :
- Fouks reconnait qu'un tel travail lui demanderait un gros effort,
- il faudrait passer obligatoirement du code pseudo 2D actuel à un code 3D complet
Point Spread Function(s) (PSFs)
PSF : point spread function, fonction d'etalement du point. C'est la convolution du lobe instrumental avec un Dirac.
À ce jour, parmi les options du programme de calcul du modèle, on peut choisir entre une PSF gaussienne et une PSF basée sur un modèle optique du satellite ISO (modèle fourni par K. Okumura, basé sur des fonctions de Bessel). Un problème clair, connu des études sur la forme des PSFs observées par ISOCAM, est que la PSF réelle n'est pas à symétrie circulaire. Néanmoins, la PSF "Bessel" analytique fournie par K. Okumura semble suffire dans un premier temps (i.e. les problèmes majeurs à ce jour ne viennent pas de la !).
Que la PSF choisie soit Gaussienne ou Besselienne, elle est décrite par 3 ou 4 paramètres, selon la manière de les compter :
- sa largeur à mi-hauteur (FWHM : Full Width at Half Maximum), cette largeur devrait être fixe pour une configuration Lentille/Filtre donnee;
- la position de son maximum (x,y) sur le pixel central (en fraction de pixel, la procédure de recherche de postion (cf ci-dessous) trouve les positions à mieux que le dixieme de largeur de pixel, avec une très faible dispersion.)
- (son amplitude au maximum)
Ajustements
Pour une configuration Lentille/Filtre donnee, la largeur à mi-hauteur devrait restee fixe (cf ) ... et les paramètres d'entree du modèle sont donc :
- la position (x,y) de la source sur le pixel central;
- l'amplitude de la source;
- le niveau du fond avant l'ajout de la source;
- le niveau du fond associé à l'ajout de la source (parce que cela correspond souvent à un changement de configuration Lentille/Filtre, en plus d'un repointage du satellite).
Les ajustements présentés ci dessous ont été fait "à la main", selon la procédure suivante :
- la configuration Lentille/Filtre donne la largeur de la PSF;
- sur les données, on estime à 1/4 de pixel-près le deplacement du centre de la source par rapport au centre du pixel central (2 inconnues de position X,Y de la source);
- sur les données, on estime le niveau du fond initial, le niveau de fond autour de la source, l'amplitude supposée finale de la source, (2 ou 3 inconnus selon les cas : niveau du fond avant et après (F1 et F2), flux de la source (FS));
- une première sortie du modèle avec les paramètres de la PSF et les 5 valeurs initiales des paramètres à trouver (x,y,F1,F2,FS) donne une indication sur les erreurs de positionnement de la source ainsi que de son amplitude
- on itère le procede en remontant aux points 1 ou 2 en fonction de l'écart données/modèle observé et on modifie soit la position, soit le niveau des flux. En general, on converge rapidement sur les niveau de flux si on se sert du comportement du pixel moyen 3x3 pour contraindre.
Figures
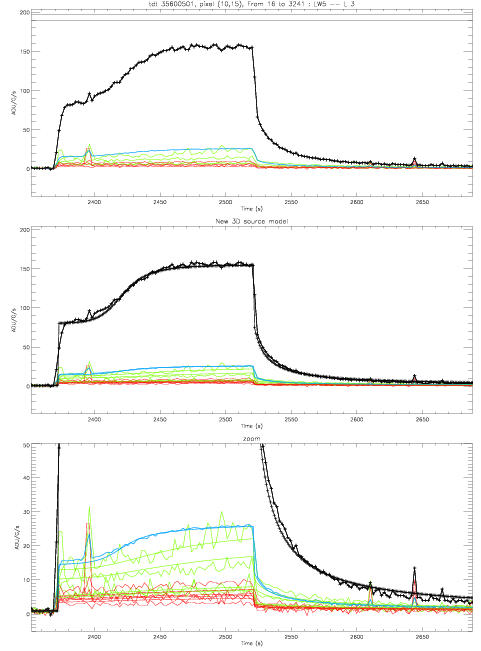
La convention sur les traces est la suivante :
- le pixel le plus brillant pour la source considérée est en noir
- les quatres plus proches voisins sont en vert
- les quatres pixels diagonaux sont en rouge
- le pixel moyen est en bleu.
Pour les courbes à 3 traces (Figures 1 à 4) :
- le trace superieur est le trace brut,
- le trace du milieu la superposition du trace brut avec la sortie du nouveau modèle de transitoires pour sources,
- le trace du bas correspondant lui à la reponse avec l'ancien modèle (modèle de reference, dit modèle Fouks-Schubert).
Tous les cubes étudiés sont echantillonnes en temps à 2.1s. Cliquez sur une image pour la voir en grand.
| Figure 1 | Figure 2 |
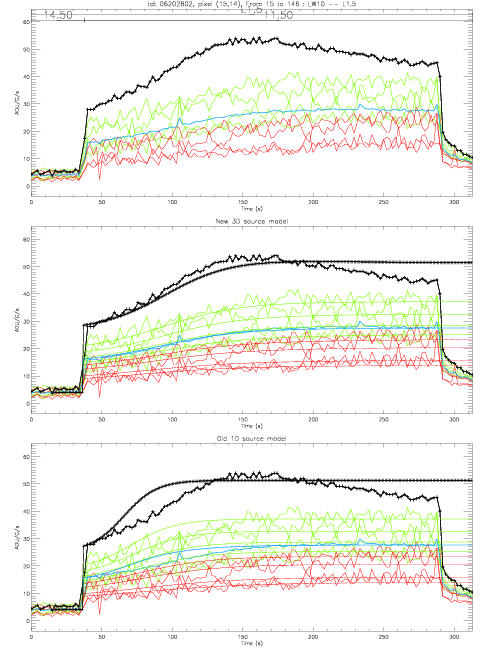
| Source large (Lentille 1.5, filtre LW 10) d'intensite moyenne | autre source large, même configuration, même ordre d'amplitude, moins de points, autre position sur le pixel |
 |
 |
| (fichier PS.gz, Taille: 80 ko) | (fichier PS.gz, Taille: 39 ko) |
| Figure 3 | Figure 4 |
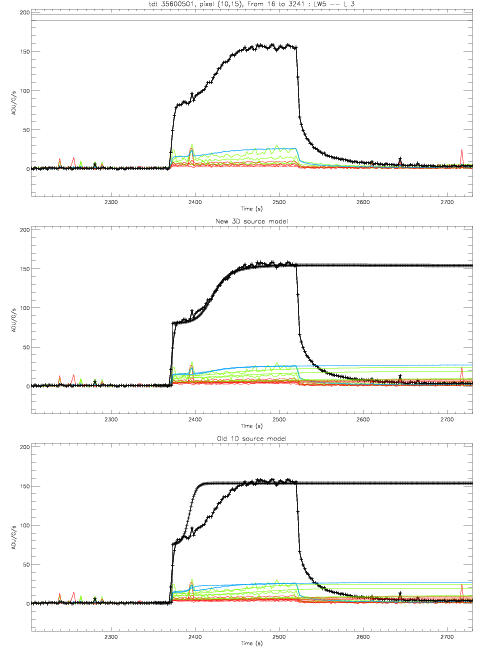
| source étroite et faible (Lentille 1.5, filtre LW 6?) | source très étroite et forte (Lentille 3, filtre LW 3) |
 |
 |
| (fichier PS.gz, Taille: 103 ko) | (fichier PS.gz, Taille: 49 ko) |
| Figure 5 | Figure 6 |
| Un exemple de description des transitoires en descente : (figure du haut : données brutes, figure du milieu : modélisation des montées et descentes, figure du bas : zoom sur la descente) | Pour les sources larges, il faut rajouter un terme correctif de premier ordre pour la première phase de montée (avant le maximum). Sur cet exemple, on a rajouté (en orange) cette correction supplémentaire. |
 |
 |
| (fichier PS.gz, Taille: 35 ko) | (fichier PS.gz, Taille: 33 ko) |
Carte des paramètres du détecteur
Le modèle décrivant les transitoires sous éclairement uniforme ne dépend que de deux paramètres fixes par pixel lies au détecteur :
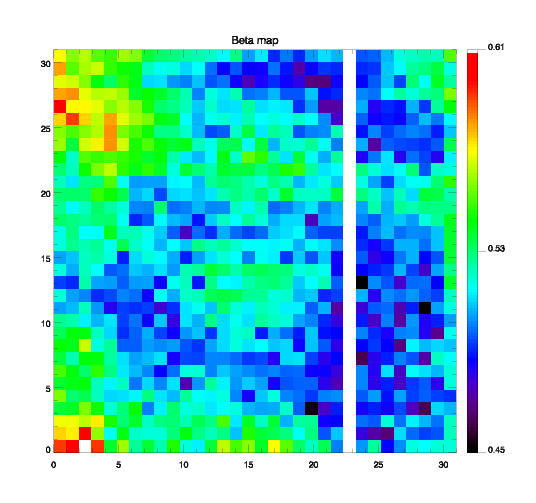
- Beta, représentant le saut instantané lors d'un changement d'illumination
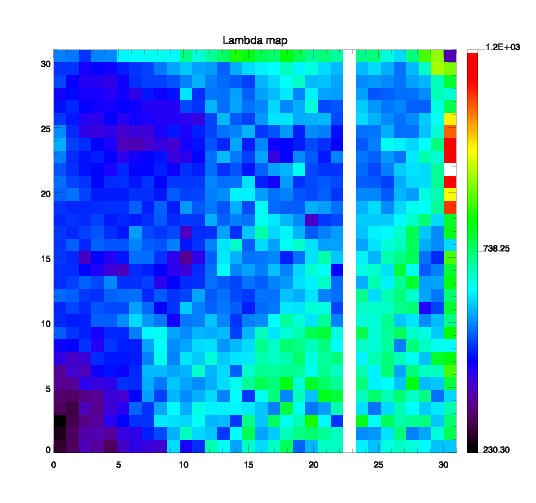
- Lambda, équivalent à une constante de temps de stabilisation du transitoire après un changement de flux incident
Le calcul de ces 2 cartes de paramètres est détaillé dans Coulais et Abergel, 2000.
Dans la théorie de Fouks, les paramètres physiques lies aux caracteristiques intrinseques du détecteur sont :
- Gain Factor, anti-correlé de la carte des Beta, paramètre décrivant la qualité du bulk pour un pixel donne (valeur moyenne du voisinage de ce pixel pour ce pixel, à cause du crosstalk électrique entre pixels);
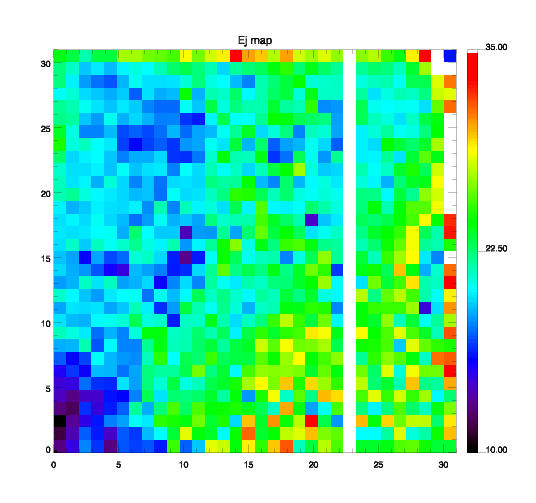
- Ej, anti-correlé de la carte des Lambda, paramètre décrivant la qualité des contacts du détecteur (c'est à dire la qualité et l'uniformite du dopage des contacts implantes dope p+).
Les équations de passage d'un couple de cartes de paramètres à l'autre sont données dans les notes de Fouks, ci-dessus.
Comme cela avait déjà été note dans Coulais et Abergel, 2000., malgré les contraintes limitant la qualité de ces cartes, la dispersion sur la carte des Beta est faible, celle sur la carte des Lambda est grande. On retrouve ceci pour la carte du Gain versus celle de Ej. Mais ces deux paramètres représentent respectivement la qualité du bulk et celle des contacts.
En conclusion, la carte du Gain Factor étant relativement uniforme avec une faible dispersion, la qualité du bulk est bonne. Par contre, la carte Ej décrivant la qualité des contacts est nettement moins bonne: il est supposé que ce paramètre n'a pas été pris en consideration lors de la fabrication de LW CAM et des test associes, en phase technologique.
;SLICE> ministats_gain_ej, gain_map, ej_map
;Gain 32*32, Mean value 1.20793
;Gain 32*32, Std . Dev. 0.0784034
;Gain [10:21]*[10:21], Mean value 1.20821
;Gain [10:21]*[10:21], Std . Dev. 0.0431217
;Ej 32*32, Mean value 22.0598
;Ej 32*32, Std . Dev. 4.32584
;Ej [10:21]*[10:21], Mean value 21.6206
;Ej [10:21]*[10:21], Std . Dev. 2.57958
;Correlation 32*32 : 0.0748885
;Correlation [10:21]*[10:21] : -0.368058
On trouvera dans les documents de Fouks des commentaires à ce sujet, donnant en particulier la voie pour concevoir et caractériser des détecteurs aussi sensible que LW-ISOCAM mais avec des constantes de temps de l'ordre de 3 à 6 fois plus rapide, et beaucoup plus uniforme de pixel à pixel ...
| Carte 32x32 des Beta | Carte 32x32 des Lambda |
 |
 |
| (fichier PS.gz, Taille: 26 ko) | (fichier PS.gz, Taille: 31 ko) |
| Carte 32x32 des Gain | Carte 32x32 de Ej | 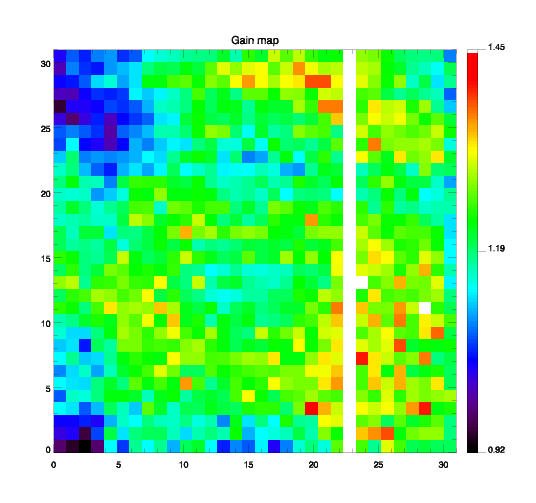 |
 |
| (fichier PS.gz, Taille: 25 ko) | (fichier PS.gz, Taille: 25 ko) |
Travaux à faire
Ces tâches sont rangées selon la progression qui parait la mieux adaptée pour aborder les questions et problèmes identifies d'après la connaisssance actuelle du sujet :
- Procédure automatique d'ajustement (Cette procédure n'a pas pour objectif de devenir la methode de correction, elle servirait a traiter "scientifiquement" --et non à la main-- et rapidement un ensemble "suffisant" de sources. À ce jour, j'ai une procédure de recherche de la position du centre de la PSF qui, readout par readout, donne d'excellents resultats, mais l'interfacage avec le programme d'ajustement ne donne pas convergence !);
- Incorporation du code correctif de 1er ordre dans le code;
- L'étude des transitoires descendants doit être reprise (cf Fig. 5). Bien souvent, le découpage des données et les modes d'observation compliquent notablement cette étude;
- étude systematique sur une jeu de sources "assez grand" pour confirmer les limites supposées du modèle, en montée comme en descente, pour differentes configurations Lentille/Filtre, amplitude de source, position, et niveaux avant et pendant;
- étude de la dépendance aux cartes 32x32 des paramètres (beta,lambda), paramètres utilises par le modèle 1D, calcules à partir de marches, avec une mauvaise dispersion pour lambda;
- étude de l'effet de mémoire (le code inclut déjà ceci, mais, comme pour l'éclairement uniforme, il faut travailler proprement pour exploiter au mieux ceci (pouvoir predicitif et qualité de correction), pour le moment, on a surtout étudié des transitoires avec une supposée stabilisation avant -même si pas seulement-);
- développement d'un code d'inversion, facilement incorporable dans les pipelines;
- Eventuel développement du code 3D et développement d'une inversion globale adaptée : on traiterait alors les observations ISOCAM orbite par orbite avec un modèle physique !
Conclusion
Le modèle a été volontairement limité à des profils quelconques à symétrie circulaire De plus, pour les sources étudiées, nous avons volontairement choisi des sources "allumées" après stabilisation.
Dans le domaine d'application du modèle, les conclusions, à ce jour, par l'étude rapide d'une dizaine de sources dans plusieures configurations Lentille/Filtre -malheureusement limitées en nombre vue le temps de recherche et celui de traitement- sont les suivantes :
- le modèle décrit parfaitement le transitoire du pixel moyen 3x3 quelque soit la configuration Lentille/Filtre pour les montées. Il reste du travail à faire pour avoir un avis definitif pour les descentes;
- le modèle décrit parfaitement les transitoires des sources les plus étroites, pixel par pixel (Lentilles 6' et 12'), en montée et en descente;
- le modèle donne des overshoots pour les sources les plus fortes et/ou les plus larges. La position des overshoots est correcte, mais le modèle sous-estime leur intensite (Lentille 1.5' et LW 10, 9, 3 ...). Fouks propose une explication physique simple à cet écart, propose un terme correctif et pourrait développer un modèle supplémentaire, demandant du temps;
- pour les PSF larges, le terme de second ordre permet d'améliorer nettement la description du transitoire montant pour le pixel le plus fort.
Rappel: ce modèle physique tourne sans nouveau paramètre, il nécessite seulement les deux cartes (beta,lambda) déjà utilisées pour le modèle décrivant les transitoires sous éclairement uniforme.